The most common sorting algorithms are:
- Insertion Sort
- Bubble Sort
- Selection Sort
- Merge sort
- Quick Sort
Insertion Sort
This is used when:
- Data set is relatively small
- Items in the data set are semi-sorted already
Worst case performance: O(n²) - So if you have 100 elements in your array, at worst, this algorithm will do 10,000 comparisons. This is when your data set is sorted completely opposite of how you wish to sort the data.
Average case performance: O(n²) - The average case won’t quite be 10,000 comparisons, but it will be higher than O(n) or O(nlogn) time.
Best case performance: O(n) - The best case performance is when the data set is already sorted and it only needs to iterate each item in the array and do one comparison for each item in the data set.
Bubble Sort
This is used when:
- When data set is relatively small
- When items in the data set are semi-sorted already
- Bubble Sort is not online (it cannot sort a stream of inputs without knowing how many items there will be) because it does not really keep track of a global maximum of the sorted elements. When an item is inserted you will need to start the bubbling from the very beginning. This could be useful, when dealing with data coming from network, or some sensor.
- Bubble sort is better than insertion sort only when someone is looking for top k elements from a large list of number i.e. in bubble sort after k iterations you'll get top k elements. However after k iterations in insertion sort, it only assures that those k elements are sorted.
Worst case performance: O(n²) - So if you have 100 elements in your array, at worst, this algorithm will do 10,000 comparisons. This is when your data set is sorted completely opposite of how you wish to sort the data.
Average case performance: O(n²) - The average case won’t quite be 10,000 comparisons, but it will be higher than O(n) or O(nlogn) time.
Best case performance: O(n) - The best case performance is when the data set is already sorted and it only needs to iterate each item in the array and do one comparison for each item in the data set.
Selection Sort
This is used when:
- When data set is relatively small
- Insertion Sort would still be more optimal as it has the possibility of fewer comparisons than Selection Sort
Worst case performance: O(n²) - The worst case is the same as both worst case, and best case. This algorithm will still need to do O(n²) comparisons to make sure everything is in order. Which is one disadvantage of this particular algorithm.
Average case performance: O(n²) - The average case is the same as both worst case, and best case. This algorithm will still need to do O(n²) comparisons to make sure everything is in order. Which is one disadvantage of this particular algorithm.
Best case performance: O(n²) - The best case performance is the same as both worst case, and average case. This algorithm will still need to do O(n²) comparisons to make sure everything is in order. Which is one disadvantage of this particular algorithm.
Merge Sort
This is used when:
- Larger data sets
- When there are not memory or storage constraints, as the most common implementations of merge sort uses a secondary list using the same amount of space as original list to help with sorting.
- When items in the data set can be accessed sequentially
- This is the only one that is stable among (Heap Sort and Quick Sort)
- Slower than the other Heap Sort and Quick Sort. Because you have to write all your data into another array and back into your original one. Copying is usually slower than comparing.
Worst case performance: O(nlogn) - The worst case is the same as both worst case, and best case.
Average case performance: O(nlogn) - The average case is the same as both worst case, and best case.
Best case performance: O(nlogn) - The best case performance is the same as both worst case, and average case.
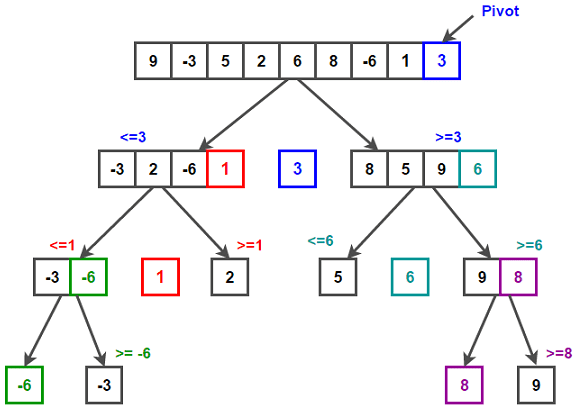
Quicksort
This is used when:
- Large data sets
- When the ordering of equal elements is not important. Quicksort is not a stable algorithm, which means that once the data set is ordered, that elements whose values are equal, are not guaranteed to be in the same ordering as the initial data set.
- Generally the fastest sorting algorithm in practice. It only swaps what needs to be swapped. Swaps are slow!
- Can be performed in-place, but in practice, the stack frames from recursive function calls results in 𝑂(log𝑛)
space complexity.
Worst case performance: O(n²) - For Quicksort, n² running time complexity is rare. This can happen in cases:
1) Array is already sorted in same order.
2) Array is already sorted in reverse order.
3) All elements are same (special case of case 1 and 2)
Average case performance: O(nlogn) - The average case is the same as best case.
Best case performance: O(nlogn) - The best case performance is the same as average case.
- Insertion Sort
- Bubble Sort
- Selection Sort
- Merge sort
- Quick Sort
Insertion Sort
This is used when:
- Data set is relatively small
- Items in the data set are semi-sorted already
Worst case performance: O(n²) - So if you have 100 elements in your array, at worst, this algorithm will do 10,000 comparisons. This is when your data set is sorted completely opposite of how you wish to sort the data.
Average case performance: O(n²) - The average case won’t quite be 10,000 comparisons, but it will be higher than O(n) or O(nlogn) time.
Best case performance: O(n) - The best case performance is when the data set is already sorted and it only needs to iterate each item in the array and do one comparison for each item in the data set.
void insertionSort(int arr[], int n) { int i, key, j; for (i = 1; i < n; i++) { key = arr[i]; j = i - 1; /* Move elements of arr[0..i-1], that are greater than key, to one position ahead of their current position */ while (j >= 0 && arr[j] > key) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = key; } }
Bubble Sort
This is used when:
- When data set is relatively small
- When items in the data set are semi-sorted already
- Bubble Sort is not online (it cannot sort a stream of inputs without knowing how many items there will be) because it does not really keep track of a global maximum of the sorted elements. When an item is inserted you will need to start the bubbling from the very beginning. This could be useful, when dealing with data coming from network, or some sensor.
- Bubble sort is better than insertion sort only when someone is looking for top k elements from a large list of number i.e. in bubble sort after k iterations you'll get top k elements. However after k iterations in insertion sort, it only assures that those k elements are sorted.
Worst case performance: O(n²) - So if you have 100 elements in your array, at worst, this algorithm will do 10,000 comparisons. This is when your data set is sorted completely opposite of how you wish to sort the data.
Average case performance: O(n²) - The average case won’t quite be 10,000 comparisons, but it will be higher than O(n) or O(nlogn) time.
Best case performance: O(n) - The best case performance is when the data set is already sorted and it only needs to iterate each item in the array and do one comparison for each item in the data set.
void bubbleSort(int arr[], int n) { int i, j; for (i = 0; i < n-1; i++) // Last i elements are already in place for (j = 0; j < n-i-1; j++) if (arr[j] > arr[j+1]) swap(&arr[j], &arr[j+1]); }
Selection Sort
This is used when:
- When data set is relatively small
- Insertion Sort would still be more optimal as it has the possibility of fewer comparisons than Selection Sort
Worst case performance: O(n²) - The worst case is the same as both worst case, and best case. This algorithm will still need to do O(n²) comparisons to make sure everything is in order. Which is one disadvantage of this particular algorithm.
Average case performance: O(n²) - The average case is the same as both worst case, and best case. This algorithm will still need to do O(n²) comparisons to make sure everything is in order. Which is one disadvantage of this particular algorithm.
Best case performance: O(n²) - The best case performance is the same as both worst case, and average case. This algorithm will still need to do O(n²) comparisons to make sure everything is in order. Which is one disadvantage of this particular algorithm.
void selectionSort(int arr[], int n) { int i, j, min_idx; // One by one move boundary of unsorted subarray for (i = 0; i < n-1; i++) { // Find the minimum element in unsorted array min_idx = i; for (j = i+1; j < n; j++) if (arr[j] < arr[min_idx]) min_idx = j; // Swap the found minimum element with the first element swap(&arr[min_idx], &arr[i]); } }
Merge Sort
- Larger data sets
- When there are not memory or storage constraints, as the most common implementations of merge sort uses a secondary list using the same amount of space as original list to help with sorting.
- When items in the data set can be accessed sequentially
- This is the only one that is stable among (Heap Sort and Quick Sort)
- Slower than the other Heap Sort and Quick Sort. Because you have to write all your data into another array and back into your original one. Copying is usually slower than comparing.
Worst case performance: O(nlogn) - The worst case is the same as both worst case, and best case.
Average case performance: O(nlogn) - The average case is the same as both worst case, and best case.
Best case performance: O(nlogn) - The best case performance is the same as both worst case, and average case.
// Merges two subarrays of arr[]. // First subarray is arr[l..m] // Second subarray is arr[m+1..r] void merge(int arr[], int l, int m, int r) { int i, j, k; int n1 = m - l + 1; int n2 = r - m; /* create temp arrays */ int L[n1], R[n2]; /* Copy data to temp arrays L[] and R[] */ for (i = 0; i < n1; i++) L[i] = arr[l + i]; for (j = 0; j < n2; j++) R[j] = arr[m + 1+ j]; /* Merge the temp arrays back into arr[l..r]*/ i = 0; // Initial index of first subarray j = 0; // Initial index of second subarray k = l; // Initial index of merged subarray while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } /* Copy the remaining elements of L[], if there are any */ while (i < n1) { arr[k] = L[i]; i++; k++; } /* Copy the remaining elements of R[], if there are any */ while (j < n2) { arr[k] = R[j]; j++; k++; } } /* l is for left index and r is right index of the sub-array of arr to be sorted */ void mergeSort(int arr[], int l, int r) { if (l < r) { // Same as (l+r)/2, but avoids overflow for // large l and h int m = l+(r-l)/2; // Sort first and second halves mergeSort(arr, l, m); mergeSort(arr, m+1, r); merge(arr, l, m, r); } }
Quicksort
This is used when:
- Large data sets
- When the ordering of equal elements is not important. Quicksort is not a stable algorithm, which means that once the data set is ordered, that elements whose values are equal, are not guaranteed to be in the same ordering as the initial data set.
- Generally the fastest sorting algorithm in practice. It only swaps what needs to be swapped. Swaps are slow!
- Can be performed in-place, but in practice, the stack frames from recursive function calls results in 𝑂(log𝑛)
space complexity.
Worst case performance: O(n²) - For Quicksort, n² running time complexity is rare. This can happen in cases:
1) Array is already sorted in same order.
2) Array is already sorted in reverse order.
3) All elements are same (special case of case 1 and 2)
Average case performance: O(nlogn) - The average case is the same as best case.
Best case performance: O(nlogn) - The best case performance is the same as average case.
// A utility function to swap two elements void swap(int* a, int* b) { int t = *a; *a = *b; *b = t; } /* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ int partition (int arr[], int low, int high) { int pivot = arr[high]; // pivot int i = (low - 1); // Index of smaller element for (int j = low; j <= high- 1; j++) { // If current element is smaller than the pivot if (arr[j] < pivot) { i++; // increment index of smaller element swap(&arr[i], &arr[j]); } } swap(&arr[i + 1], &arr[high]); return (i + 1); } /* The main function that implements QuickSort arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */ void quickSort(int arr[], int low, int high) { if (low < high) { /* pi is partitioning index, arr[p] is now at right place */ int pi = partition(arr, low, high); // Separately sort elements before // partition and after partition quickSort(arr, low, pi - 1); quickSort(arr, pi + 1, high); } }

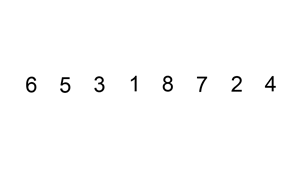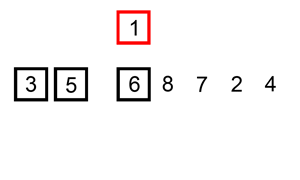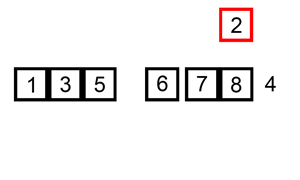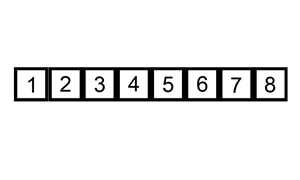






Không có nhận xét nào:
Đăng nhận xét